第5课时平面向量的坐标运算、
平面向量共线的坐标表示
基础达标
1.下列说法中正确的个数是.
①向量在平面直角坐标系xOy内的坐标是唯一的;
②若![]() =,则
=,则![]() 的终点坐标是;
的终点坐标是;
③若![]() 的终点坐标为,则
的终点坐标为,则![]() =.
=.
A.0B.1 C.2 D.3
【分析】由于i,j为正交基底,所以①正确;向量的坐标与表示该向量的有向线段的始点、终点的具体地方无关,只与其相对地方有关,故②③不正确.
【答案】B
2.已知a=,b=,当a∥b时,实数x的值是.
A.3 B.4 C.5 D.6
【分析】由于a=,b=,且a∥b,所以×1-2×2=0,解得x=5.
【答案】C
3.若平面直角坐标系内的两个向量a=,b=,且平面内的任一向量c都可以唯一的表示成c=λa+μb,则实数m的取值范围是.
A. B.
C. D.∪
【分析】由题意知,向量a与b不共线,所以3m-2-2m≠0,即m≠2.
【答案】D
4.已知点A,B,向量![]() =,则向量
=,则向量![]() =.
=.
A. B.
C. D.
【分析】设点C的坐标为,∵A,![]() =,
=,
∴![]() 解得
解得![]()
∴点C的坐标为.
又B,∴![]() =,故选B.
=,故选B.
【答案】B
5.已知![]() =,
=,![]() =,
=,![]() =,若A,B,C三点共线,则实数k=__________.
=,若A,B,C三点共线,则实数k=__________.
【分析】由题意,得![]() =,
=,![]() =.
=.
由于A,B,C三点共线,所以-6×7=0.
解得k=-2或k=11.
【答案】-2或11
6.设向量![]() 绕点O逆时针旋转
绕点O逆时针旋转![]() 得到向量
得到向量![]() ,且2
,且2![]() +
+![]() =,则向量
=,则向量![]() =__________.
=__________.
【分析】设![]() =,则
=,则![]() =,所以2
=,所以2![]() +
+![]() ==,即
==,即![]() 解得
解得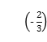 因此,
因此,![]() =
=![]() .
.
【答案】![]()
7.已知A,B,C三点的坐标分别为,,,且![]() =
=![]() ,
,![]() =
=![]() ,求证:
,求证:![]() ∥
∥![]() .
.
【分析】设E,F,
依题意有![]() =,
=,![]() =,
=,![]() =.
=.
∵![]() =
=![]() =
=![]() ,
,
![]() =
=![]() =
=![]() ,
,
又=![]() ,
,
∴x1=-![]() ,y1=
,y1=![]() ,即E
,即E![]() .
.
又=![]() ,
,
∴x2=![]() ,y2=0,即F
,y2=0,即F![]() ,∴
,∴![]() =
=![]() .
.
∵4×![]() -
-![]() ×=0,
×=0,
∴![]() ∥
∥![]() .
.
拓展提高
8.已知在▱ABCD中,点A,B,C,则点D的坐标为.
A. B.
C. D.
【分析】设点D的坐标为,
∵四边形ABCD是平行四边形,∴![]() =
=![]() .
.
又∵![]() =,
=,![]() =,
=,
∴1-x=4且-5-y=0,∴x=-3,y=-5.
故点D的坐标为.
【答案】D
9.在平面直角坐标系中,O为坐标原点,已知点A,B,若点C满足![]() =α
=α![]() +β
+β![]() ,其中α,β∈R,且α+β=1,则点C所在直线方程为.
,其中α,β∈R,且α+β=1,则点C所在直线方程为.
A.3x+2y-11=0 B.2x+y-5=0
C.2x-y=0 D.x+2y-5=0
【分析】设点C,则![]() =,
=,![]() =,
=,![]() =.
=.
由![]() =α
=α![]() +β
+β![]() ,得=+=,
,得=+=,
于是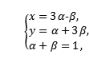 消去α,β得x+2y-5=0.
消去α,β得x+2y-5=0.
由平面向量共线定理知,当![]() =α
=α![]() +β
+β![]() ,α+β=1时,点A,B,C共线.
,α+β=1时,点A,B,C共线.
因此点C的轨迹为直线AB,故所求轨迹方程为x+2y-5=0.
【答案】D
10.若点O为坐标原点,且点A,B,C的坐标分别为,,,则直线AC与直线OB的交点P的坐标为__________.
【分析】设交点P的坐标为,
由于P为直线AC与直线OB的交点,所以点P在直线OB上,
所以![]() 与
与![]() 共线.
共线.
又![]() =,
=,![]() =,
=,
所以4x-4y=0,即x-y=0,①
同理,![]() 与
与![]() 共线.
共线.
由于![]() =,
=,![]() =,
=,
所以×6+2y=0,即6x+2y-24=0,②
联立①②,解得x=3,y=3,故点P的坐标为.
【答案】
11.已知点A,B,点P在直线AB上,且|![]() |=2|
|=2|![]() |,求点P的坐标.
|,求点P的坐标.
【分析】设点P的坐标为,|![]() |=2|
|=2|![]() |,
|,
当点P在线段AB上时,![]() =2
=2![]() ,
,
∴=2,
∴![]() 解得
解得![]()
∴点P的坐标为![]() .
.
当点P在线段AB的延长线上时,![]() =-2
=-2![]() ,
,
∴=-2,
∴![]() 解得
解得![]()
∴点P的坐标为.
综上所述,点P的坐标为![]() 或.
或.







